Geometri och vinklar
En fråga om geometri och vinklar?
En sexkant med alla sidor raka och lika långa, hur många graders vinkel får sexkantens hörn?
TRÅDSTARTARENS TILLÄGGSKOMMENTAR 2019-10-12 14:52
Formen som avses är mutterformen.
-
-
Svar på tråden Geometri och vinklar
-
Om du mäter med gradskiva på två av sidorna över ett hörn visar gradskivan 60 grader, jag uppfattade det som ts ville veta detta.möjligt skrev 2019-10-11 08:57:01 följande:
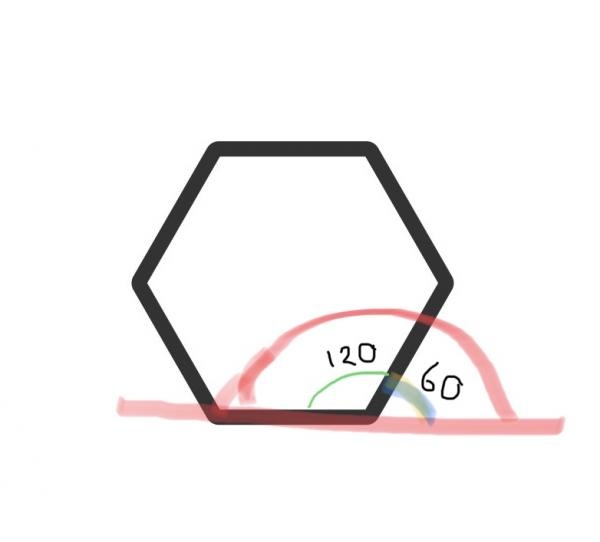
Antingen talar du om komplementvinkeln som ligger utanför hexagonen eller den vinkel som blir mellan linjen och hexagonens sida om du drar en linje tvärs över hexagonen från ett hörn till motstående hörn.
-
Vänligen visa var du hittar en skarpt spetsig vinkel på en mutter med 6 sidor.Giftskåneman skrev 2019-10-11 08:57:05 följande:
Skaffa dig en gradvinkel och mät en mutter.
-
Anonym (Popcorn) skrev 2019-10-11 09:37:27 följande:
Vänligen visa var du hittar en skarpt spetsig vinkel på en mutter med 6 sidor.
Hittepånick, du har otur då du tänker.
-
Detta är vad jag gissar att du mäter. Isf är det komplementvinkeln som är 60 grader. Men du får gärna skissa eller ta en bild på vad du menarGiftskåneman skrev 2019-10-11 09:10:15 följande:
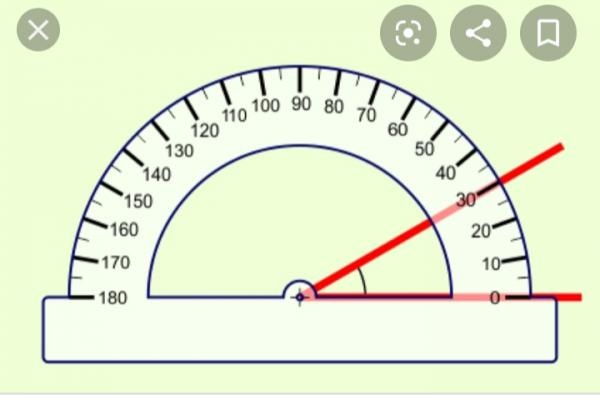
Om du mäter med gradskiva på två av sidorna över ett hörn visar gradskivan 60 grader, jag uppfattade det som ts ville veta detta.
-
Om någon kommer fram till annat än 60 grader så har ni skolkat på matten!
Summan i alla dessa olika former är alltd 360 grader, sedan är det ju inte så svårt att divivera det med antal hörn.... -
Det är bara din teori som, tur är.Giftskåneman skrev 2019-10-11 08:04:54 följande:Tillverka du din hexagon efter din teori, så ska jag göra min efter min teori. Lycka till, som du resonerar går det inte
Dessutom, hittepånick, så tragiskt.
Vågar du inte stå för dina åsikter här? -
Kverulant67 skrev 2019-10-11 10:58:27 följande:Om någon kommer fram till annat än 60 grader så har ni skolkat på matten!
Summan i alla dessa olika former är alltd 360 grader, sedan är det ju inte så svårt att divivera det med antal hörn....Han räknar på andra sidan av sträcket, möjligtvis har han rätt om man leker semantik.
Men agerar man i matten, nej!
Men borde finnas något namn för räkna vinklarna på utsidan, eller?
-
Helt santKverulant67 skrev 2019-10-11 10:58:27 följande:
Om någon kommer fram till annat än 60 grader så har ni skolkat på matten!
Summan i alla dessa olika former är alltd 360 grader, sedan är det ju inte så svårt att divivera det med antal hörn....
Om man talar om komplementvinklarna vilket inte alls är det TS frågar efter .
Formeln för en liksidig månghörningens vinklar borde Dock kunna skrivas som (180-(360/n))
Annars hade alla dessa geometriska former definitionsmässigt haft samma vinkelsumma(360 grader). Man måste följa definitions konventionen och då är polygonens hörnvinkel inom(!) polygonen -
Heter det komplementvinklar om man mäter på utsida av figuren?möjligt skrev 2019-10-11 11:05:06 följande:Helt sant
Om man talar om komplementvinklarna vilket inte alls är det TS frågar efter .
Formeln för en liksidig månghörningens vinklar borde Dock kunna skrivas som (180-(360/n))
Annars hade alla dessa geometriska former definitionsmässigt haft samma vinkelsumma(360 grader). Man måste följa definitions konventionen och då är polygonens hörnvinkel inom(!) polygonen -
[quote=79955634][quote-nick]Giftskåneman skrev 2019-10-11 10:51:18 följande:[/quote-nick][/quote]
Eftersom det är du som i ett tidigare inlägg hävdar att man från en tänkt mittlinje till, jag förmodar du menar ett hörn, kan få en vinkel om 30 grader så är det väl bara att rita upp vart du hittar denna? Att vrida och vända för att hitta en 60 graders vinkel funkar, men ej en 30 graders.