Geometri och vinklar
Giftskåneman skrev 2019-10-10 15:05:36 följande:
Vad är det då?
Inlägg från: möjligt
|
-
120
-
Peta in en mittpunkt i sexkanten. Dra sedan streck från mittpunkten till varje hörn. Då har du sex likbenta trianglar. Eftersom summan av alla ?topp?vinklarna blir 360(helt varv) så ser man att trianglar är liksidiga och varje vinkel 60 grader. Man ser också omedelbart att ett sexkantshörn utgörs av två triangelvinklar -> 60+60=120grader
-
Exakt vilken vinkel är det då du mäter?Giftskåneman skrev 2019-10-10 15:25:14 följande:
Mäter du med en gradskiva på en liksidig 6 kant är varje vinkel 60 grader
-
-
Pratar du om yttervikeln som bildas mellan hexagonen och linjen man förlänger en av sidorna?Giftskåneman skrev 2019-10-10 15:25:14 följande:
Mäter du med en gradskiva på en liksidig 6 kant är varje vinkel 60 grader
-
Har för mig att denna kan benämnas komplementvinkel och snvänds ibland inom byggmöjligt skrev 2019-10-10 15:31:33 följande:
Pratar du om yttervikeln som bildas mellan hexagonen och linjen man förlänger en av sidorna?
-
Ja det är det jag benämner komplementvinkeln, för den är komplementet från polygonens innervinkel till den räta linjen som bildas om man låter sidanforsätta. Med en polygonsvinklar menar man alltid de vinklar som ligger inom polygonen.Giftskåneman skrev 2019-10-10 16:16:34 följande:
Nä, vinkeln är totalt 60 grader mätt från sidorna
-
Du får nog ta en bild på en liten skiss och visa vilka vinklar det är du mäter. Drar du olika raka streck inom sexhörningen så kan du ju självklart skapa både 60 graders och 30 graders vinklar men ingen är dessa vinklar är ensam en är sexhörningens vinklar, dens egna vinklar är 120 grader. Kantlängden och vinklarna definierar den .Giftskåneman skrev 2019-10-11 07:32:48 följande:
Eller så förstår du inte det jag påpekar
-
Fast exakt vilka andra skapade vinklar i hexagonen man använder för att tillverka den är inte relevant för frågan. Frågan I TS är:Giftskåneman skrev 2019-10-11 08:14:05 följande:
Tillverkar hexagoner varje vecka, en del av mitt jobb, och för att få den rätt används graderna jag angett. Ibland är måtten från hörn till hörn, ibland är måtten hörn till hörn genom centrum, ibland måtten mellan två plana sidor.
En sexkant med alla sidor raka och lika långa, hur många graders vinkel får sexkantens hörn?
Det finns inget tolkningsutrymme för den frågan. En polygons vinklar är definitionsmässigt den inre vinkeln som bildas mellan två ihopsatta sidor. Se inlägg 36.
Det förvånar mig inte alls att det inte är 120 gradersvinkeln man mäter ifrån när man skapar en, som jag nämnde är det mycket lättare att utgå ifrån tex komplement vinkeln eller 6 liksidiga trianglar som sitter ihop i toppen(hexagonens centrum).
Menar du att en sexkants hörn är 60grader? För det är vad TS frågar. Skulle du försöka rita den geometrin skulle du sluta med en liksidig triangel där du går över varje sida 2 ggr, dvs två varv på triangeln. -
Antingen talar du om komplementvinkeln som ligger utanför hexagonen eller den vinkel som blir mellan linjen och hexagonens sida om du drar en linje tvärs över hexagonen från ett hörn till motstående hörn.
-
Detta är vad jag gissar att du mäter. Isf är det komplementvinkeln som är 60 grader. Men du får gärna skissa eller ta en bild på vad du menarGiftskåneman skrev 2019-10-11 09:10:15 följande:
Om du mäter med gradskiva på två av sidorna över ett hörn visar gradskivan 60 grader, jag uppfattade det som ts ville veta detta.
-
Helt santKverulant67 skrev 2019-10-11 10:58:27 följande:
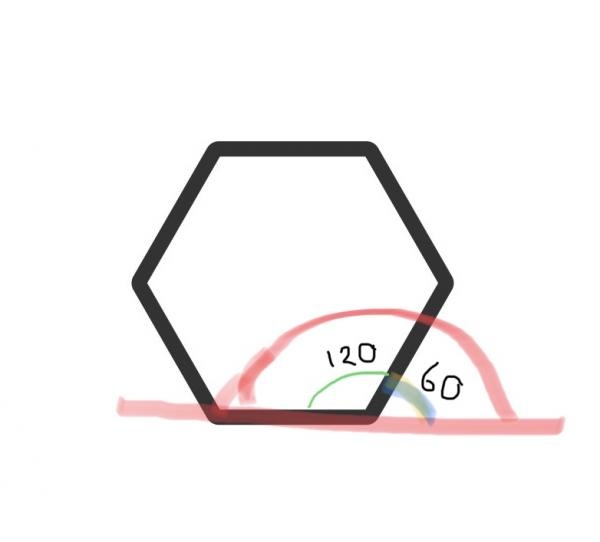
Om någon kommer fram till annat än 60 grader så har ni skolkat på matten!
Summan i alla dessa olika former är alltd 360 grader, sedan är det ju inte så svårt att divivera det med antal hörn....
Om man talar om komplementvinklarna vilket inte alls är det TS frågar efter .
Formeln för en liksidig månghörningens vinklar borde Dock kunna skrivas som (180-(360/n))
Annars hade alla dessa geometriska former definitionsmässigt haft samma vinkelsumma(360 grader). Man måste följa definitions konventionen och då är polygonens hörnvinkel inom(!) polygonen -
Halva vinkeln är 30 grader.Giftskåneman skrev 2019-10-11 12:23:55 följande:
Eftersom det är du som i ett tidigare inlägg hävdar att man från en tänkt mittlinje till, jag förmodar du menar ett hörn, kan få en vinkel om 30 grader så är det väl bara att rita upp vart du hittar denna? Att vrida och vända för att hitta en 60 graders vinkel funkar, men ej en 30 graders.
Har sett på bilderna här att min benämning på gradskiva varit felaktig, inte sån vi mäter med, benämningen är olika hos olika leverantörer, låt oss säga graderad smygvinkel, eller vinkelmätare istället[/quote]
Du får kalla det vad du vill, fortfarande mäter du yttervinkeln. Inte polygonens innervinklar vilket är det man menar i sammanhanget. -
Matematiskt är komplementvinkeln den som kompletterar till 90 grader men i praktiska sammanhang använder man ibland begreppet om den typen av yttervinklar jag markerat i figuren, den blir då ett komplement till 180 grader istället för 90klyban skrev 2019-10-11 11:13:26 följande:
Heter det komplementvinklar om man mäter på utsida av figuren?
-
Det kan vara praktiskt ibland. Tänka dig själv att du vill montera en sexhörning av tex bräder, då blir det mycket enklare att kunna lägga ett mätverktyg med utsidan och ha denna som referens och stöd när du vill veta hur riktningen på nästa del ska vara. Bara en sådan sak som att du kan ha sexhörningen liggande ovanpågradskivan gör det ju mycket enklare att se var män faktiskt mäter, iom. att konventionen ger att du mäter vinklar moturs från horisontalplanet.klyban skrev 2019-10-11 13:54:43 följande:
Varför vill han räkna på detta sätt?
Förstår inte poängen med det.
Kanske inte ni gör heller.
Han gör inga större ansträngning att bevisa nått heller, så det kommer nog bli en lång nonsens diskussion.
-
Förstår faktiskt inte riktigt vad du eller han menar men det är ju ett praktiskt och smart sätt att räkna och det ger en enkel formel för både innervinklarna:(180-(360/n))klyban skrev 2019-10-11 14:37:21 följande:
Jojo, den praktisk delen och såga senare, den köper vi, och tänkt på.
Men tänkte mer i denna diskussion som få 360grader till nått annat.
Vart är den logisk poängen där och i själva matten?(Och då giftskånemans påståenden)
För om detta bra var saken, så borde man redan varit överens, tex där man äter utsida så ökar gradantalet runt om.
Och att det andra är alltid 360grader oavsett hur många vinklar.
Varför gör han den distinktionen i matten?
Eller är det bortom din förmåga och förstå också.
Att det är bortom min förmåga att förstå utan hjälp, håller inte på med matte,inte gjort på evigheter.'
Så är rätt rostig, därav alla frågor.
Och en enkel formel för vinkelsumman för hela polygonen n*(180-(360/n))=180*(n-2).
Men att ett hörns vinkel är det som ligger på insidan är inget att debattera om så båda sätten fungerar fint men det gäller att ha koll på vad den faktiska frågan var som skulle bli besvarad -
Förstår faktiskt inte riktigt vad du eller han menar men det är ju ett praktiskt och smart sätt att räkna och det ger en enkel formel för både innervinklarna:(180-(360/n))klyban skrev 2019-10-11 14:37:21 följande:
Jojo, den praktisk delen och såga senare, den köper vi, och tänkt på.
Men tänkte mer i denna diskussion som få 360grader till nått annat.
Vart är den logisk poängen där och i själva matten?(Och då giftskånemans påståenden)
För om detta bra var saken, så borde man redan varit överens, tex där man äter utsida så ökar gradantalet runt om.
Och att det andra är alltid 360grader oavsett hur många vinklar.
Varför gör han den distinktionen i matten?
Eller är det bortom din förmåga och förstå också.
Att det är bortom min förmåga att förstå utan hjälp, håller inte på med matte,inte gjort på evigheter.'
Så är rätt rostig, därav alla frågor.
Och en enkel formel för vinkelsumman för hela polygonen n*(180-(360/n))=180*(n-2).
Men att ett hörns vinkel är det som ligger på insidan är inget att debattera om så båda sätten fungerar fint men det gäller att ha koll på vad den faktiska frågan var som skulle bli besvarad